二叉树的前中后序非递归遍历方式
前序、中序、后序遍历的顺序其实指的是根结点在遍历树时候的位置；
左子树 右子树
| | |
根（前序） 根（中序） 根（后序）
T94. Binary Tree Inorder Traversal 使用迭代的方式，中序遍历一棵树。 步骤：1、由根节点向左子树依次查找，直到子结点不包含左子树，将经过的左子结点全部放到栈中；2、弹栈，获取栈的顶层结点，这就是中序遍历得到的第一个结点；3、因为该结点已经没有左子树，因此该节点就可以看做左子树为NULL，并且该根节点可能存在右子树的一个根节点，此时要沿着这个节点的右子树进行遍历，得到右子树的第一个子结点（也就是右子树的根节点），右子树可以以该根节点为根，重复过程1-3，对右子树进行中序遍历。
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if(!root)
return res;
stack<TreeNode*> s;
TreeNode* curr=root;
while(curr!=NULL||!s.empty()) {
if(curr!=NULL) {
s.push(curr);
curr=curr->left;
}
else {
curr=s.top();
s.pop();
res.push_back(curr->val);
curr=curr->right;
}
}
return res;
}
T144. Binary Tree Preorder Traversal 使用迭代的方式前序遍历一棵树 步骤：1、从根节点开始向左子树进行深入，直接将经历的左子树加入到结果数组中，同时将遍历的左子结点添加到栈中；2、左子树为空的时候，由于“最外面的树 ”根节点和左子树已经遍历完成，只剩下右子树，直接弹栈得到上面一层的左子结点，得到左子结点的右子树；3、重复步骤1-3，直到遍历到的所有的子树结点和栈同时为空的时候即遍历完整棵树。
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if(!root)
return res;
stack<TreeNode*> s;
TreeNode* curr=root;
while(curr!=NULL||!s.empty()) {
if(curr) {
res.push_back(curr->val);
s.push(curr);
curr=curr->left;
}
else {
curr=s.top();
s.pop();
curr=curr->right;
}
}
return res;
}
T145. Binary Tree Postorder Traversal 使用迭代的方式后续遍历一棵树 基本思路：后序遍历：left-right-root 实现：root-right-left，每次向得到的数组中插入数值的时候插入到数组的第一个位置，于是得到left-right-root的顺序。 步骤：1、创建栈，将根结点压栈；2、将根结点弹栈，左子结点入栈，右子结点入栈；3、将栈中的元素依次弹出，这样实现root-right-left的遍历顺序，每次将遍历到的元素插入数组的起始位置，得到结果
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
if(!root)
return res;
stack<TreeNode*> s;
s.push(root);
TreeNode* curr;
while(!s.empty()) {
curr=s.top();
s.pop();
res.insert(res.begin(), curr->val);
if (curr->left)
s.push(curr->left);
if (curr->right)
s.push(curr->right);
}
return res;
}
上面的方法有点 cheating的意思，换一个方法思路：
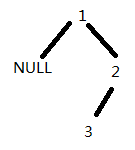解释if(curr->right && curr->right!=prev)：首先栈内被填满s = [1,2,3]，之后s弹出 3 2，到1 的时候，如果不判断是否已经遍历过 结点 2的话，此时程序又会将 结点2 加入到s中，导致程序发生超时错误；
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
TreeNode *prev = NULL, *curr = root;
stack<TreeNode*> s;
while(curr || !s.empty()) {
while(curr) {
s.push(curr);
curr = curr->left;
}
curr = s.top();
if(curr->right && curr->right!=prev) { // 防止重复向右子树遍历，考虑[1,null,2,3]的情况
curr = curr->right;
}
else {
result.push_back(curr->val);
s.pop(); // when you pop a node from stack, you ensure you have already explored its children
prev = curr;
curr = NULL; // 不是s.top()栈顶的值，而是NULL
}
}
return result;
}
二叉树的递归题
T226. Invert Binary Tree 将一颗二叉树进行左右翻转： 思路：从上到下遍历整颗二叉树，第一层不用交换，第二层的两个结点需要交换1次，第三层的子结点需要交换2次
TreeNode* invertTree(TreeNode* root) {
//使用栈，相当于广度优先的方式，不断从上至下遍历这棵树
if(!root)
return root;
stack<TreeNode*> s;
s.push(root);
//遍历
while(!s.empty()) {
TreeNode* curr=s.top();
s.pop();
//节点存在才能将左右子结点压入栈中，不加条件判断会导致栈中永远存在空结点
if(curr) {
s.push(curr->left);
s.push(curr->right);
swap(curr->left, curr->right);
}
}
return root;
}
T110. Balanced Binary Tree 判断一个树的所有的左右子树的高度是否相差1：
bool isBalanced(TreeNode* root) {
if(!root) return true;
int left = depth(root->left);
int right = depth(root->right);
// 用黑盒的方法来想象：
return abs(left-right)<=1 && isBalanced(root->left) && isBalanced(root->right);
}
// 判断一棵树的高度
int depth(TreeNode* root) {
if(!root)
return 0;
return max(depth(root->left), depth(root->right)) + 1;
}
T129. Sum Root to Leaf Numbers 从树的根结点到叶子结点组成一个数字，将这颗树中所有这样的数字求和（树的递归题目，画一颗深度为3 的二叉树，将自己写的递归函数带进去，就能看出结果！）：
int sumNumbers(TreeNode* root) {
if(!root) return 0;
return sumNumbers(root, 0);
}
int sumNumbers(TreeNode* root, int val) {
if(root->left==NULL&&root->right==NULL)
return 10*val+root->val;
int res=0;
if(root->left)
res+=sumNumbers(root->left, 10*val+root->val);
if(root->right)
res+=sumNumbers(root->right, 10*val+root->val);
return res;
}
T199. Binary Tree Right Side View 从一颗树的右边来观察这棵树，得到结果
vector<int> rightSideView(TreeNode* root) {
//广度优先遍历这棵树是可以的，但是想用深度优先，递归的方式来搞
vector<int> res;
if(!root) return res;
rightSideView(res, root, 0);
return res;
}
void rightSideView(vector<int> &res, TreeNode* root, int depth) {
if(!root) return;
if(depth==res.size()) res.push_back(root->val);
rightSideView(res,root->right,depth+1);
rightSideView(res,root->left,depth+1);
}
T230. Kth Smallest Element in a BST 找到二叉搜索树中第k小的数：
int kthSmallest(TreeNode* root, int k) {
//解决这种问题，画一颗BST就好分析
int leftNodes = countNodes(root->left);
if(k<=leftNodes) {
return kthSmallest(root->left, k);
}
else if(k==leftNodes+1) {
return root->val;
}
else if(k>leftNodes+1){
return kthSmallest(root->right, k-leftNodes-1);
}
}
//统计树中的结点数目
int countNodes(TreeNode* root) {
if(!root) return 0;
return 1+countNodes(root->left)+countNodes(root->right);
}
T236. Lowest Common Ancestor of a Binary Tree 二叉树中两个结点的最近的公共祖先，不要深入想这个递归流程，还是将这个递归看成黑盒
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root) //遍历到当前子树的时候，根结点已经为NULL
return NULL;
if(root==p||root==q) //遍历到当前子树的时候，根结点为想要找的p或者q，返回root，表明在树的该条链路上面找到p或者q
return root;
//如果遍历到当前的根结点不是p也不是q，那么需要在当前根结点的左右子树中深入查找
TreeNode* left=lowestCommonAncestor(root->left, p, q);
TreeNode* right=lowestCommonAncestor(root->right, p, q);
//有三种情况：pq都不在左子树上(返回右子树)，pq都不在右子树上(返回左子树)，pq一个在左子树一个在右子树，那么就需要返回当前节点
if(!left)
return right;
if(!right)
return left;
if(left&&right)
return root;
}
总结
- 递归函数，参数的确定很重要，每次递归的时候只会改变参数（参数+1传递到下一层，一般参数中会含有树的深度，不要把树的深度定义为递归函数的变量，要把深度定义为参数，参数的引用增加元素等等）
- 终止条件的判断：
if(root==NULL) return; if(xxx) result.push_back(root->val); //递归公式，向树的深层次递归
